LDAの各変数の意味と幾何的解釈について
はじめに
LDAの仕組みについて,時間をあけるとすぐに記憶が飛んでしまうためメモ.
ここでは以下についてまとめます*1
- LDAのグラフィカルモデルにおける各変数の意味とは?
- LDAは幾何的に何をやってるのか?
LDAのグラフィカルモデル
まず,各文書についてBag of Words(BoW)表現に変換する*2.
そして,次の仮定をおく.
これをグラフィカルモデルに落としこむと下図になる*5.
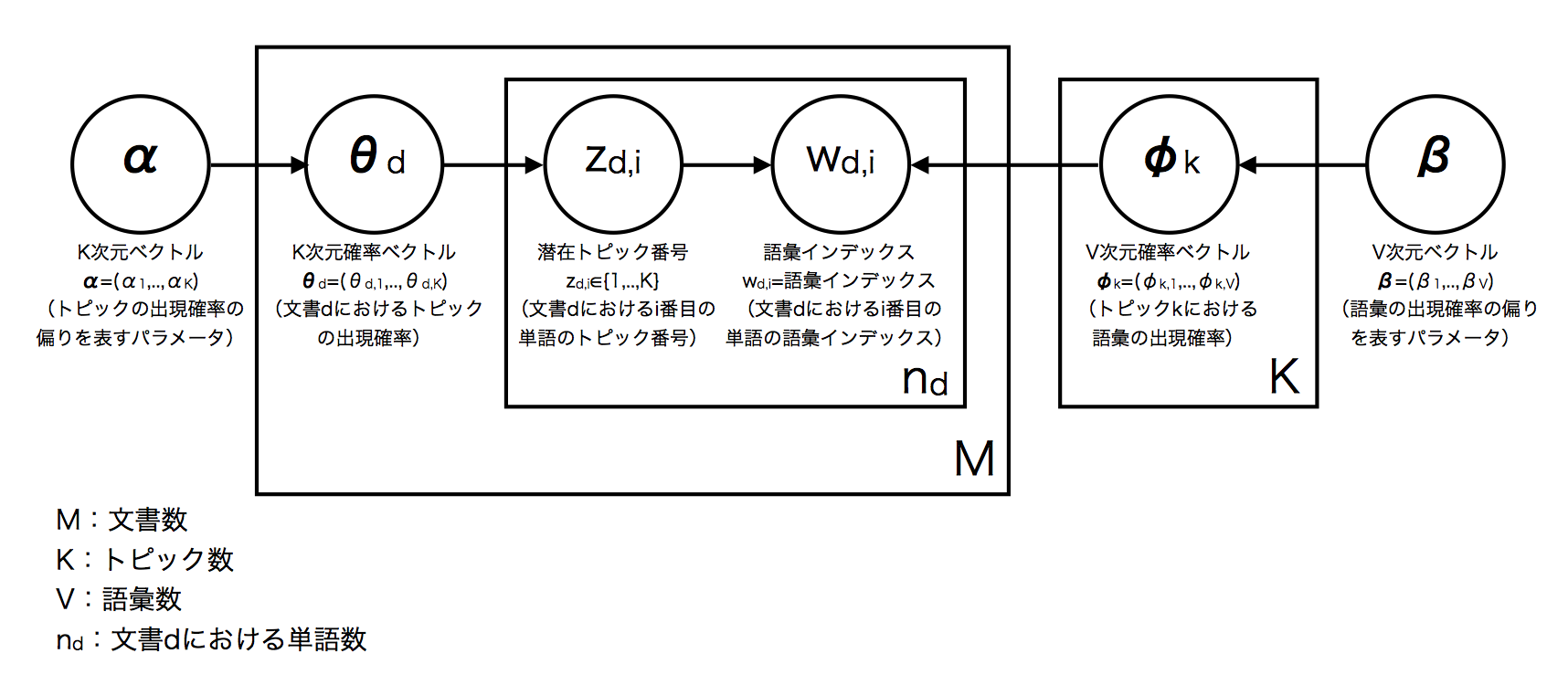
すると,グラフィカルモデルにおける各変数の意味は次のようになる.*6
:文書数
:文書集合全体におけるトピック数
:文書集合全体における語彙数*7
:文書dにおける単語数*8
:文書
における
番目の単語の語彙インデックス*9
:文書
における
番目の単語の潜在トピック
:文書
におけるトピックの出現確率ベクトル.
:トピックの出現頻度の偏りを表すパラメータ*10
:トピック
における語彙の出現確率ベクトル.
:語彙の出現頻度の偏りを表すパラメータ*11
LDAの生成過程
ただし,はディリクレ分布,
は多項分布を表す.*12
また,と
はパラメータとして与える.
補足:パラメータ と
と の意味
の意味
多項分布による生成過程を考えて,
の事前分布としてディリクレ分布
,ただし
を考える.
すると,の事後分布は,
となる.
ただし,は
回試行の中で
が出現した回数.
すなわち,事前分布におけるは,事後分布では
に加算される.
したがって,はデータを観測する前の
ごとの仮想的頻度を表す.
よって,LDAにおけると
についていえば,次のようになる.
は,トピックの出現頻度の偏りを表すパラメータ
は,語彙の出現頻度の偏りを表すパラメータ
LDAの幾何的解釈
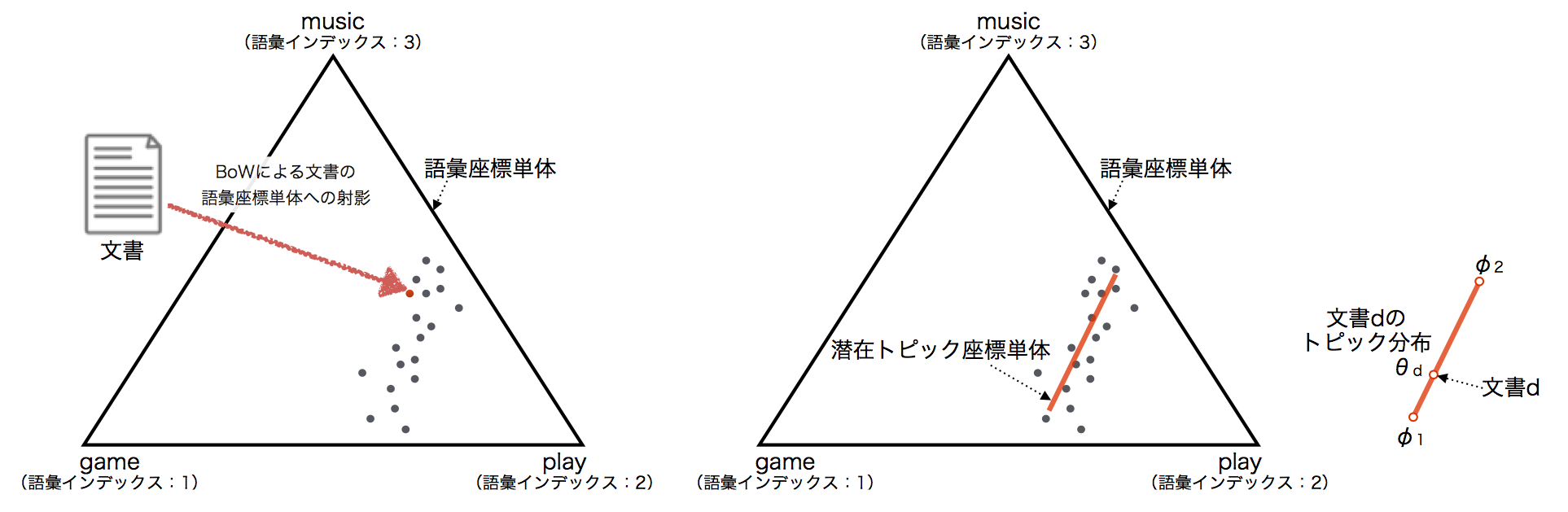 簡単のため,全文書集合における語彙数Vが3の場合を考える*13.
簡単のため,全文書集合における語彙数Vが3の場合を考える*13.
このとき,各文書をBoW表現にすることで,上図の語彙座標単体*14に射影できる.
各文書は語彙座標単体空間に偏りをもって分布していると想定*15され,より低次元に射影できるはずである.
この低次元空間(単体)を潜在トピック座標単体と呼び,その基底ベクトルがトピックとなり,トピックは語彙の出現確率分布で表現される.そして,各文書のトピック分布は,潜在トピック座標単体上の点となる.
つまり,LDAのは,文書集合の潜在トピック座標単体上への射影とみることができ,
潜在トピック座標単体は,単語座標単体よりも低次元であるため次元圧縮と見ることができる.
参考文献

トピックモデルによる統計的潜在意味解析 (自然言語処理シリーズ)
- 作者: 佐藤一誠,奥村学
- 出版社/メーカー: コロナ社
- 発売日: 2015/03/13
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (5件) を見る
*1:ほとんどの内容を本ページ末尾の参考文献から引っ張ってきています
*2:文書を形態素解析し,形態素のヒストグラムに変換する.例えば,文書が「もももすももももものうち」であれば,分かち書き「もも/も/すもも/も/もも/の/うち」に対して,形態素ごとにカウントした「もも:2 も:2 すもも:1 の:1 うち:1」がBoW表現である.
*3:話題.音楽,スポーツ,政治…など
*4:出現箇所が異なればその単語のトピックは異なる.例えば,「アップルが新製品を発表しました」と「バナナ,アップル,キウイのミックスジュースがうまい」の「アップル」のトピックは異なる.前者は「企業」トピックとしてのアップルであり,後者は「フルーツ」トピックとしてのアップルである.
*5:これは正確にはSmoothed LDAのグラフィカルモデル.無印LDAの場合はβが存在しない.多くの場合,LDAといえばSmoothed LDAを指すみたい.
*6:ベクトル表記に関して,上図では太字で記し,下では矢印で表記する.…はてなtex記法で太字を表現できなかった…
*7:ここでは「語彙」はユニークな形態素として呼び,一方「単語」はユニークでない形態素として呼ぶ.例えば,「もももすももももものうち」の語彙数は「もも」「も」「すもも」「の」「うち」の5つとするのに対して,単語数は「もも」「も」「すもも」「も」「もも」「の」「うち」の7つとする.
*8:語彙数とは異なるので注意
*9:語彙インデックスは語彙へのマッピング情報を持つ.例えば,語彙インデックス「3」は語彙「すもも」を表すなど
*10:要素値は大きくなるに連れて,文書集合全体においてトピック
が出現しやすくなる
*11:要素値は大きくなるに連れて,文書集合全体において語彙インデックス
の語彙が出現しやすくなる
*12:各分布の意味はこちらのスライドがわかりやすいです → 3分でわかる多項分布とディリクレ分布 - http://www.slideshare.net/stjunya/ss-29629644/4
*13:すべての文書において,登場する語彙がgame,play,musicの3つしか存在しない状況
*14:各語彙の出現確率の総和が1となるような空間
*15:単語には共起性があるから